12 KiB
On Separators and Structure
When analyzing elements within a ARC Puzzle, a certain distinction is necessary when classifying the role this objects play on the solution.
There are figure-like elements that are the main focus of problem, usually objects that are central to the proposed transformation, while others play a secondary role.
In this document, I propose a simple, non-exaustive, classfication of these support elements into two families: Box-Separator and Structure. These families contain subcategories with their own forms representations.
Proposed Classification
- Box-Separator
- Full-Length Line
- Vertical
- Horizontal
- Borders
- Combination of Line Segments
- Full-Border
- Frames
- Borderless Frames
- Filled Frames
- Negative Space
- Full-Length Line
- Structure
- Objects
- Block
- Permeability
- Grids
- Objects
Box-Separators Family
Definition of Box-Separator Objects
Box-Separators are common visual elements that create logical divisions within the grid, establishing independent panels that function separately from each other. Unlike structural elements (grids, blocks), Box-Separators define boundaries between distinct problem spaces, often separating instructions from the working area, or dividing sequential steps in a transformation process.
These separators can appear as full-length lines, bordered regions, or filled frames, but they consistently serve to isolate parts of the puzzle that should be processed independently or understood as separate logical units.
A panel is a subdivided part of the grid that creates an independent space. A different grid withih the grid no direct connecting elements between the parts. That is not the same as not relationship, but elements cannot cross the divisor or intereact with each other directly.
The Separators Usage
Separators serve to:
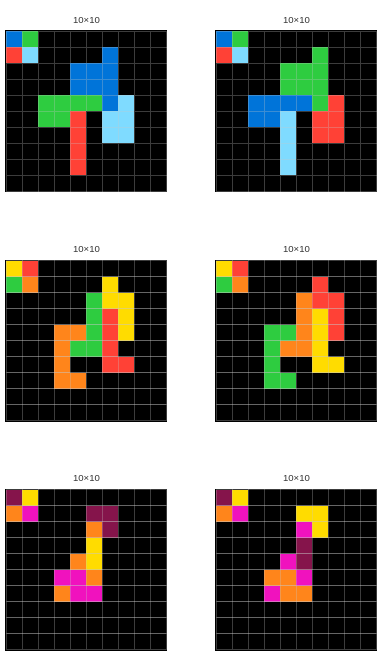
1. Divide the Problem into complementary parts
2. Divide into Sequences (time)

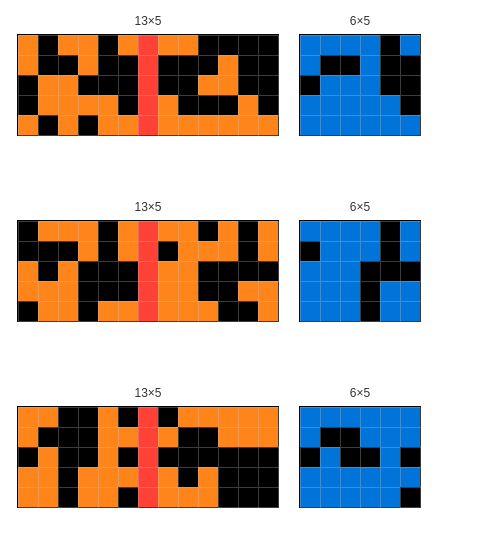
3. Isolate In-grid Instructions
4. Highlight or Isolate an Area within an element

The Separator Formats
They can be presented in different forms like: 1. Full-Length Lines (Vertical/Horizontal)

2. Combination of Line Segments

3. Borders (An Outline of a Quadrilateral)
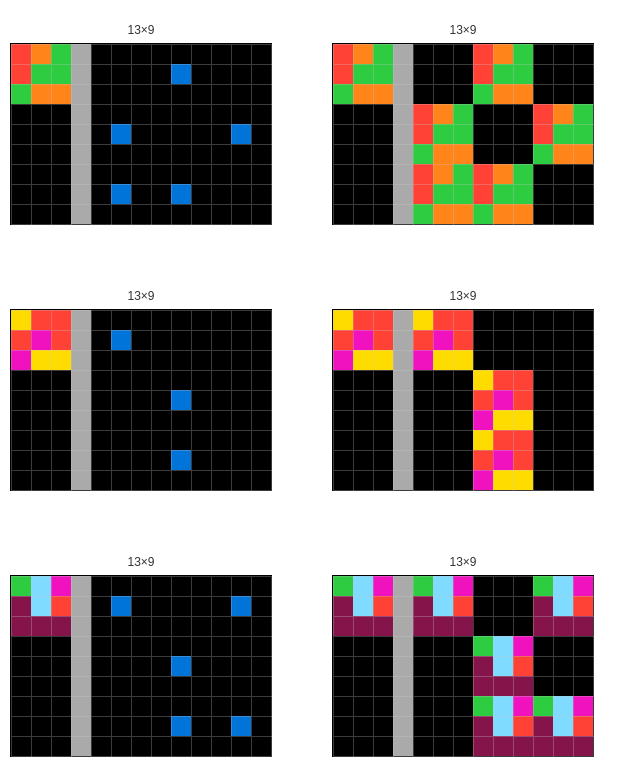
4. Frame (A Solid Quadrilateral)
Negative Space

Structure
Grids Objects
A conceptually different function can be argued in the form of the Grid, which serves as structure, not actual separation. We will address this issue further below.
Analyzing Box-Separator Lines Cases
Equal Sized Panels
The easiest case is detecting Box-Separators that split the grid into two equal sized panels. It also uses a specific color, distinct from the rest of the grid.
Horizontal Example (27a77e38):

Vertical Example (195ba7dc):

Although it is a simple rule, this is not generalizable to all problems, since Box-Separators may divide the grid into asymmetrical panels.
Different Sized Panels (Asymmetrical)
Here is an asymmetrical example of Box-Separator line:
Example 1: 2b01abd0
On 2b01abd0, the left panel is 6 cells wide, while the right side is only 5.
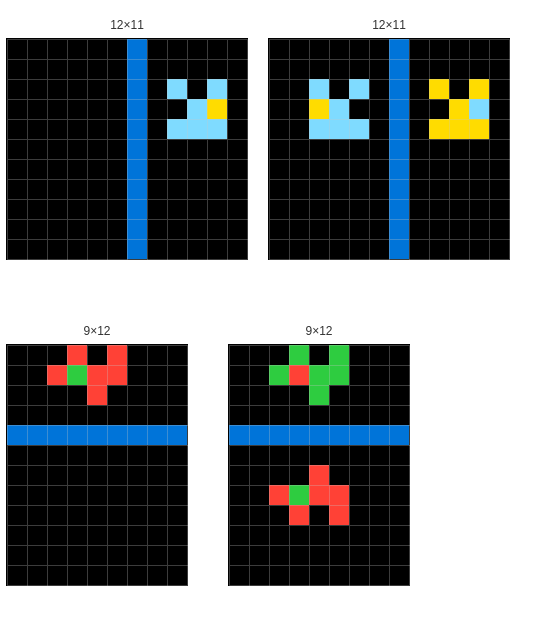
Example 2: AboveBelow1
On AboveBelow1, the top panel is 6 cells high, while the bottom one is only 4:

Proposing Rules to Solve this Ambiguity
Observing the selected problems, it becomes apparent that usually the Box-Separator Line has the following properties:
Rule 1: Full Length Line
If we are considering 'Lines' this is a given.
Obs: Could there be a Non-Full Length line separtor? Maybe, I still need to find the example.
Rule 2: Consistency
Since the Box-Separator Line must be present in the Input Grids (learning), we will consider this one of the core rules. Its representation on the output grid is optional, and there are plenty of examples where it is only represented on the input grid.
We have yet to find examples where a Box-Separator is used solely in the output grid as part of transformation, while not being present in the input.
It not only must be present in the input grid, but actuall in ALL of the input grids. If there is an element that could be interpreted as a Box-Separator Line, but is only present in one or not in all learning grids, this would effectively make it NOT a valid for Box-Separator.
The reasoning behind this one is a bit empirical: in order to achieve a non-ambiguous solution, a certain uniformity of elements must be present. Having problems with such a distinct layout together (box separated) with ones that don't feature this characteristic seems very implausible.
Rule 3: Distinct Color
In a similar sense, the color must also be distinct enough to not cause ambiguity. So, Box-Separator Lines must use a distinct color from the rest of the elements, making them very easy to determine. Distinct in relationship to the background and other elements.
Could Black be a Box-Separator Line? As we have discussed in our conference, theoretically yes, but we have yet to see such example. This would void this rule, or at least provide some changes in way that the color distinctiveness would be related to the other elements but not background.
Example HERE
Testing the Proposed Rules
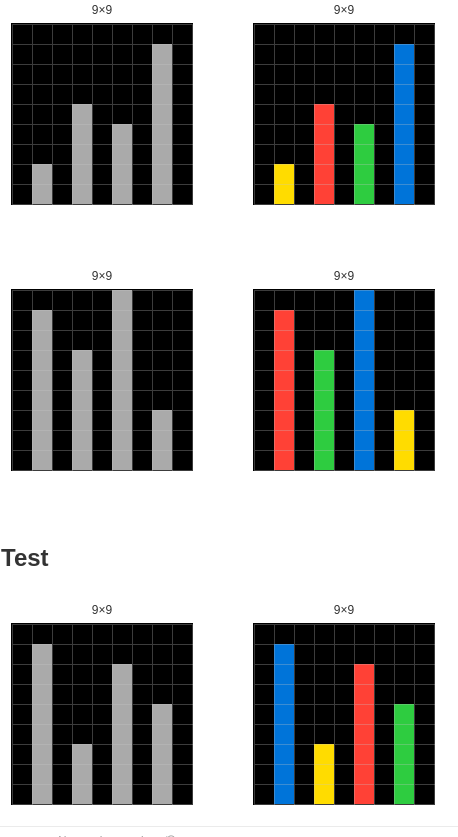
Test #1: 08ed6ac7
Puzzle 08ed6ac7 is quite challenging, since it contains an element that splits the grid into two panels vertically, but clearly, for humans, is not a Box-Separator Line:
Using the proposed rules:
✅ Rule 1: Full Length Line In the second example, the third (left-to-right) vertical bar is a full length line.
❌ Rule 2: Consistency Only one of the examples on the input grid (learning) contains the Box-Separator Line, failing the consistency rule
❌ Rule 3: Distinct Color If we consider the input grid (learning), we only have gray bars. If we would ONLY look at the output grid (apply), we couldn't determine if blue is a distinct color from the rest of the elements.
Conclusion: By failing both rules, we can assert that the vertical element present in one of the grids is not a Box-Separator.
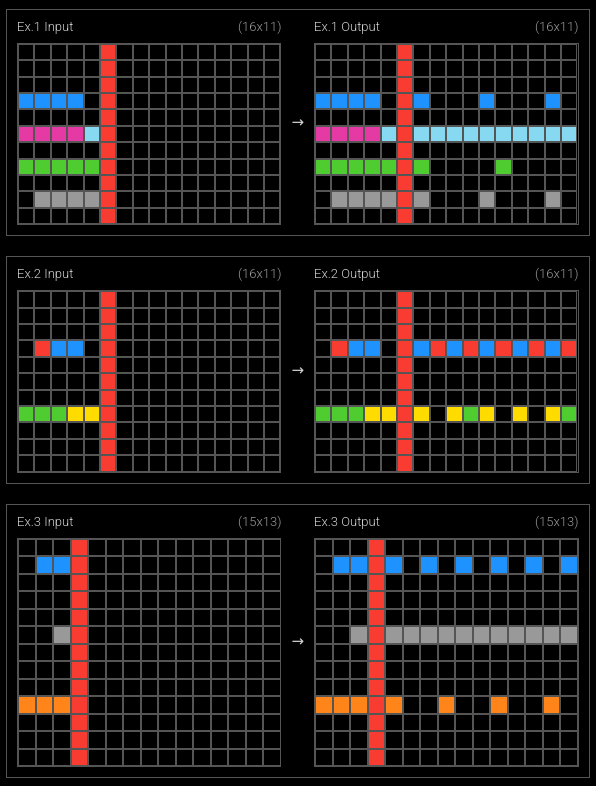
Test #2: 363442ee
Puzzle 363442ee employs a Box-Separator line to divide the grid into two panels, one containing an element and the other with individual pixels that indicate where the element should be reproduced.
Using the proposed rules:
✅ Rule 1: Full Length Line The vertical gray bar is a full-length line.
✅ Rule 2: Consistency Box-Separator Line is present in all learning examples (Input)
✅ Rule 3: Distinct Color The Box-Separator Line is gray, a distinct color from the rest of the elements
Conclusion: With all conditions met, we can validate that the problem does indeed contain a Box-Separator Line.
Test #3: Barrier with Alternating Color (0bb8deee)
Test #4: Complex Case of Structure and Frame (15113be4)
Test #5: Multiple Divisions (351d6448)
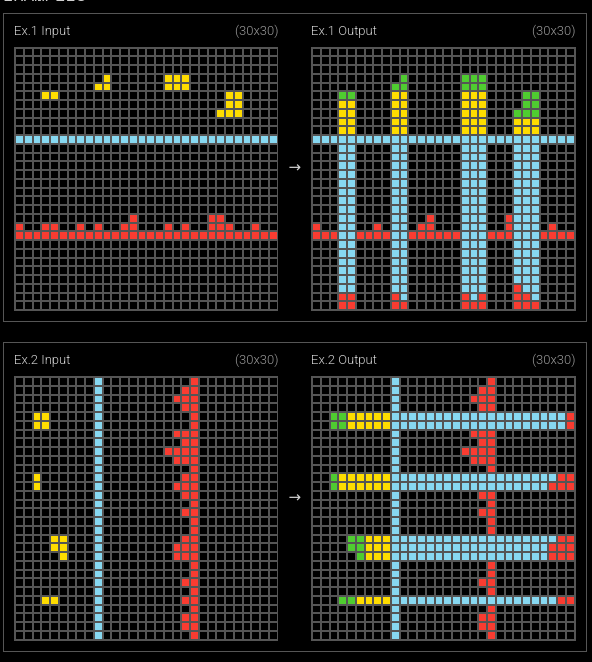
There are also puzzles that use multiple divisions using Box-Separator Lines. For example, 351d6448 employs 4 horizontal box-separator lines to create smaller panels.
Could we still apply the proposed rules?
Using the proposed rules:
✅ Rule 1: Full Length Line The horizontal gray bar is a full-length line.
✅ Rule 2: Consistency Box-Separator Line is present in all learning examples (Input)
✅ Rule 3: Distinct Color The color selected gray is uniquely used for the separator.
Conclusion: Satisfying the proposed rules, we can assert it does indeed contain a Box-Separator Line.
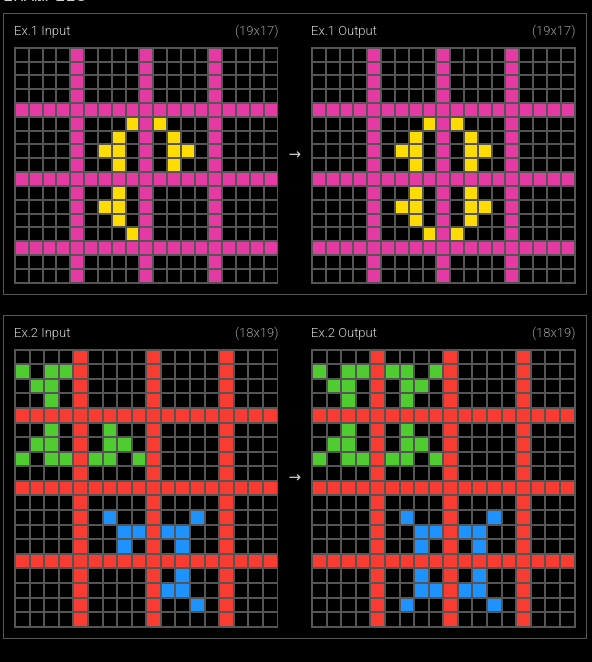
Test #6: Grid-like Division (39e1d7f9)
This one could be argued to be a different case, since the Box-Separator is not dividing the problems in n parts, but actually serving as structure for the rest of the elements.
In previous examples, the separator was used to logically divide the grid into panels that share some sort of relationship. In this case it merely serves as a divider.
So conceptually they are different, but let's still try to apply the rules established.
Using the proposed rules:
✅ Rule 1: Consistency Box-Separator Line is present in all learning examples (Input)
✅ Rule 2: Distinct Color The color selected in all examples is uniquely used for the separator, not shared by any other element.
Note: While technically valid, I would still argue that this is a different concept.
Additional Examples of Structure
Distinct Frame
Test #7: Invisible Box-Separator Line (009d5c81)
Frames as Separator Structures
ARC is filled with many cases where separators are present, but not only in line form. Frames are also part of the objects used to deliberately separate a part of the puzzle into different logical parts.
A very common case is the key or legend, which contains instructions on how to operate the transformation, but are not necessarily part of the transformation and remain unchanged or disappear in the output.
Example 1: Frame (1e81d6f9)
This is very similar to the ones presented so far, the major difference is that instead of a line, we have two segments of a line that isolate the top-left corner, forming a little frame.
✅ Rule 1: Consistency ✅ Rule 2: Distinct Color
Even here we could still apply both rules (Consistency and Color), validating that this is indeed a Box-Separator-X*
[] X is used here intentionally to substitute "Lines" in the original conceptualization.*
Example 2: Frame (2f0c5170)
This one is a bit of a departure from the previous ones. It uses frames (light blue) to isolate the background into two parts. Similar, although different to negative space.
Or is the background light-blue and the frame is black?
✅ Rule 1: Consistency ✅ Rule 2: Distinct Color
The rules would still apply (Consistency and Color), but another aspect to be evaluated is the different width used. Lines and Frames have a consistent line width, which is not clear here.
Conceptually, I think it is the same as the previous examples, just its implementation is a bit different.
Non-Full-Length Lines
(find Examples)